F-Test

The low F-statistic of 0.27 says the variation within the appraisers is greater than the variation between them. The F-critical value is 2.81.

You can use the F-table above to get a close estimate of the F-critical value. One downfall with tables is sometimes the table may not provide a precise number since not every combination is shown. However, the table can provide a fairly good estimate and at least allow a decision to be very conclusive.

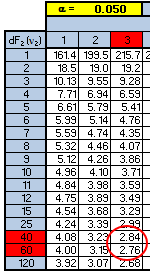
The numerator has 3 degrees of freedom and the denominator has 48 degrees of freedom. Using the table below shows that the F-critical value is going to be between 2.76 and 2.84. And in this case, both values are much higher than the F-calculated value of 0.27 so the conclusion is the same.

As a Six Sigma project manager it may be worth re-running (depending on cost and time) the trial with a larger sample size and additional appraiser training to reduce the variation within each one.

The variation is fairly consistent among each of them so it appears there is a systemic issue that is causing nearly similar amounts of variation within each appraiser.

It is possible that one or a few of the widgets are creating the similar spread in the timing for each appraiser. You may examine the timing performance of each widget and run an ANOVA among the 13 widgets and see if one or more stands out.

Epsilon-squared is the % of variation related to the Factor, which is the Appraiser. This is 4.84 / 291.69 = 0.01659 = 1.7%. This is a low value, so it is possible that other Factors exist that are creating the variation.