Six Sigma Material ... simplified |
The newest material for July 2025 includes updates on the topics of:
- Practice Lean Six Sigma Certification Exam
- Rational subgrouping and why it is important
- Takt Time & Loading
DMAIC - click on a phase below
Six Sigma Templates and Calculators
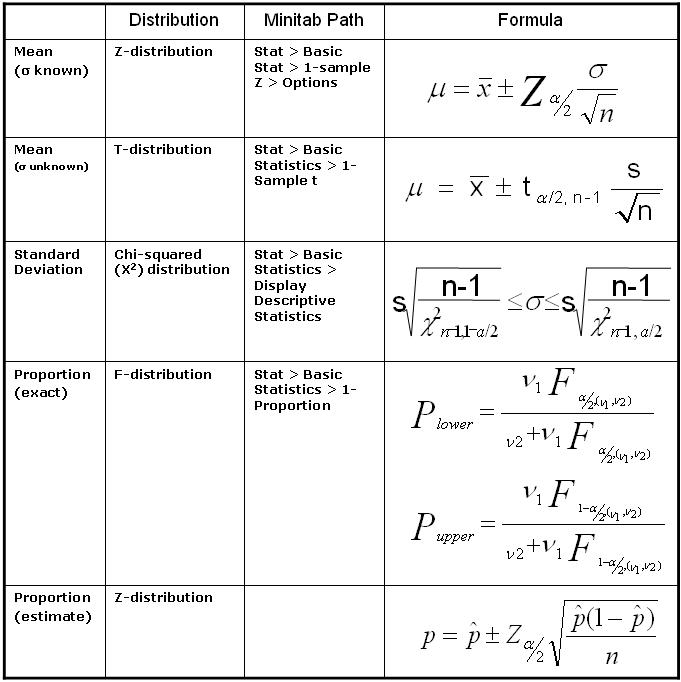
A collection of templates, tables, and calculators allow you to run quick calculations, model scenarios, make your job quicker and easier, and help close your project. Many come with detailed examples. Formulas for the calculations can be made visible...which are also beneficial in preparing for a certification exam.
Complete Site Access + more
Get complete access to Six-Sigma-Material.com, free downloads, practice exam questions, and more. Thousands of pages explaining the various Six Sigma and Lean Manufacturing tools with new information added monthly.
Subscribers get unrestricted access to all the pages within the site.
Click here to learn more.
|
MONTHLY membership $12/month |
ANNUAL membership $42/year |
The Six Sigma Methodology
Learning all of the Six Sigma material through any certification course or tutorial can be overwhelming and challenging.
Not familiar with Six Sigma? Click here to learn what many CEO's and others are learning and adopting for their companies.
Thoroughly understanding the array of continuous improvement tools, their value, and meaning takes more time and application than a course allows. This material is presented in a simple format to help comprehend the basic principles in smaller lessons.
This site is also designed to help those use their training and skillsets to find a career. Click here to search for job openings related to Six Sigma.
This website will provide clarity and knowledge of each step of the process through the use of visual aids and roadmaps. Understanding the basics is essential prior to leading a team as a White Belt, Yellow Belts, Green Belt, Black Belt, Master Black Belt, or any other type of continuous improvement leader and project manager.
The tools provide the project team with guidance; they will not directly improve the process. Proper employment of the tools will guide critical decisions and monitor control. Understanding when and which to apply will accelerate project execution.
The methodology is disciplined and structured. There are frequent applications of statistical tests but being overly number bound has its limitations. The results of statistical tests should be checked and balanced with reason.... ask the question "do the statistical results make practical sense?
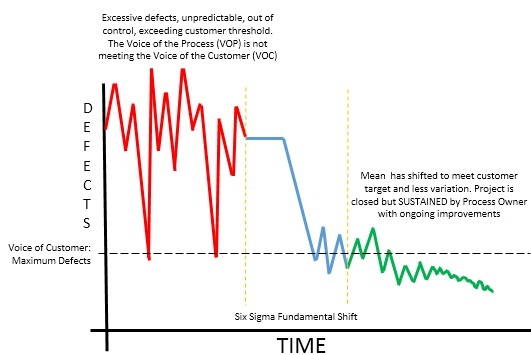
Much of the traditional emphasis of quality improvement and continuous improvement programs is placed on waste reduction and shifting process performance toward a target. The Six Sigma methodology strives to achieve more...and sustain the achievement.
Six Sigma is a collection of these tools applied in a systematic manner with an emphasis on variation reduction for process improvement (DMAIC) and product development (DFSS)
Six Sigma is a business management strategy for which its foundation is typically credited to engineer Bill Smith at Motorola in 1986. The program picked up momentum through substantial gains from another engineer, Jack Welch Jr., while serving as CEO of General Electric.
Six Sigma in an Organization
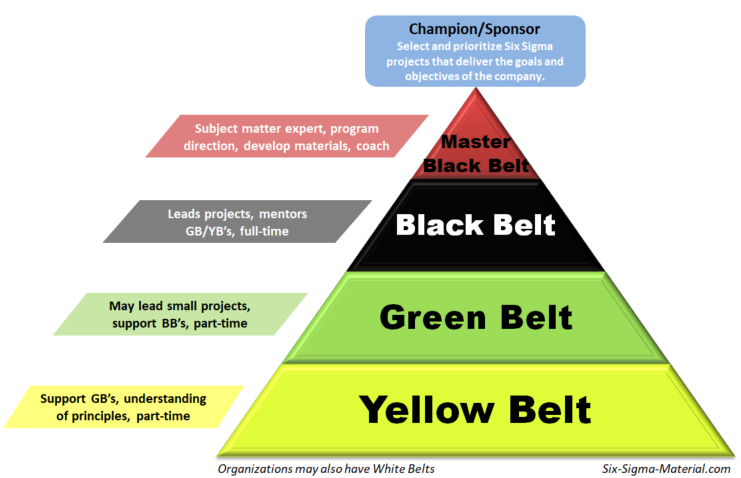
A Six Sigma program within a company usually creates its own infrastructure. Six Sigma "Belts" are often thought to be those with engineering backgrounds. While there are many that succeed due to their statistical background it is certainly not the requirement. In fact, each company should train a wide variety of backgrounds as their change agents to lead the company on the Six Sigma journey.
Candidates should come from human resources, finance, clerical, operations, sales, marketing, quality control, engineering, production control, purchasing, supply chain, R&D, maintenance, and any other department within an organization.
The CEO (or owner) and Board of Directors are at the highest level of a corporation. They have decided to embrace and implement the methodology in their company.
Upper Management representative or Vice-President of Six Sigma They are responsible for all the inputs and outputs (profits related to Six Sigma projects) of the program reporting to the CEO.
Champions or Sponsors are leaders trained to select and prioritize Six Sigma projects that deliver the goals and objectives of the company. Champions will select and mentor Six Sigma project leaders such as Black Belts and Green Belts.
Champions are frequently engaged in the beginning of DMAIC and DFSS projects in the Define phase to ensure the scope is being maintained and going in the right direction.
Master Black Belts
Master Black Belts (MBB) report to the VP of Six Sigma and are the highest level of "belt". Some may specialize in DMAIC, DFSS, or both methodologies but they are subject matter experts in Six Sigma material with advanced statistical knowledge.
Companies that focus a lot of resources on research and development may be more interested in DFSS experts. Those that are process oriented may have a need for more DMAIC experts. MBB's may lead some projects that are very large in scope with a high impact to the organization. They are also responsible for teaching programs, development of materials, and the Six Sigma certification program.
The MBB's are the high-level teachers of Six Sigma material as well as Black Belts. The effectiveness and use of the tools is a reflection of an organization's teachers. When the learners haven't learned, the teachers haven't taught. The proper application of the methodology starts with the MBB's.
Six Sigma Black Belts (SSBB)
Black Belts (BB) work for the MBB. They are usually full time Six Sigma employees carrying out the duty of a change agent. Black Belts work projects smaller in scope than the MBB but larger than the Green Belts (GB). Black Belts are also be subject matter experts and will often conduct training, mentoring, and develop new six sigma material.
Often a BB will lead a team that has Green Belts as team members, but GB's are not required. It is more important to engage critical stakeholders of the project that are willing to accept change and participate. With cross-functional representation the subjective component of the methodology will add more value.
Black Belts have usually been selected as high caliber talent and capable of leading transformation. The technical skills are half of the skillset, being able to change the culture and manage the project is the other.
Six Sigma Green Belts (SSGB)
Green Belts often lead projects themselves, and normally have an assigned Black Belt as a mentor. These teams may have other Green Belts and also include stakeholders such as operators, supervisors, human resources, finance, and anywhere else in the company.
Anyone with a stake in the outcome and is willing to participate can be on the team. Green Belts often continue to hold their existing job and responsibilities while leading a project.
Six Sigma Yellow Belts (SSYB)
Yellow Belts typically go through about 15-20 hours of training and an exam. At this secondary level are the introduction of metrics and basic improvement methodologies. Yellow Belts retain their existing job and participate on Six Sigma teams as needed and will have responsibilities from data collection, waste identification, to basic statistical analysis.
Six Sigma White Belts (SSWB)
White Belts are trained in general principles of Six Sigma and Lean Manufacturing. Certification usually requires one day of training and an exam. When this level exists within a company's Six Sigma infrastructure it is considered the first level. White belts become accustomed to the structure and format of a DMAIC or DFSS project.
Recent Articles
-
Process Capability Indices
Oct 18, 21 09:32 AM
Determing the process capability indices, Pp, Ppk, Cp, Cpk, Cpm -
Six Sigma Calculator, Statistics Tables, and Six Sigma Templates
Sep 14, 21 09:19 AM
Six Sigma Calculators, Statistics Tables, and Six Sigma Templates to make your job easier as a Six Sigma Project Manager -
Six Sigma Templates, Statistics Tables, and Six Sigma Calculators
Aug 16, 21 01:25 PM
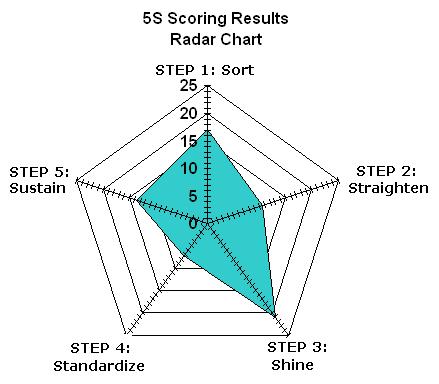
Six Sigma Templates, Tables, and Calculators. MTBF, MTTR, A3, EOQ, 5S, 5 WHY, DPMO, FMEA, SIPOC, RTY, DMAIC Contract, OEE, Value Stream Map, Pugh Matrix

Site Membership
LEARN MORE
Six Sigma
Templates, Tables & Calculators
Six Sigma Slides
Green Belt Program (1,000+ Slides)
Basic Statistics
Cost of Quality
SPC
Control Charts
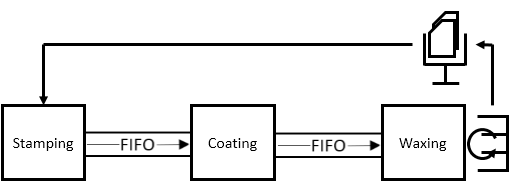
Process Mapping
Capability Studies
MSA
SIPOC
Cause & Effect Matrix
FMEA
Multivariate Analysis
Central Limit Theorem
Confidence Intervals
Hypothesis Testing
Normality
T Tests
1-Way ANOVA
Chi-Square
Correlation
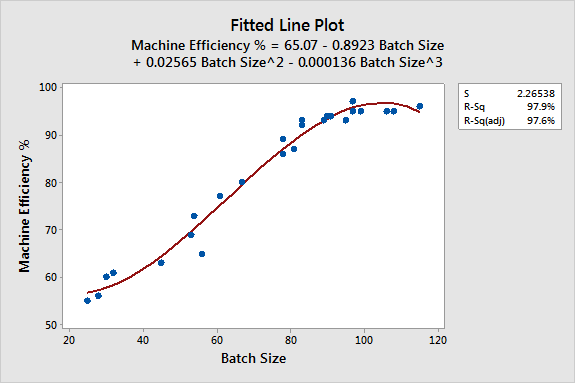
Regression
Control Plan
Kaizen
MTBF and MTTR
Project Pitfalls
Error Proofing
Z Scores
OEE
Takt Time
Line Balancing
Yield Metrics
Sampling Methods
Data Classification
Practice Exam
... and more