Kurtosis
Shape of the Distribution

There are three types of kurtosis which is a description of the "peakedness" or "flatness" of the probability distribution curve relative to the bell curve of a normal distribution. This does not have to do with skewness.

1) Platykurtic - negative kurtosis value indicating a flatter distribution that normal bell curve. The lower the value the flatter the distribution with more spread. An example is the Uniform Distribution which has a kurtosis = -1.2.

2) Leptokurtic - positive kurtosis value indicating a peaked shaped distribution compared to normal bell curve. The higher the value the sharper the peak the distribution and less spread. An example is the Double Exponential Distribution which has a kurtosis = 3.

3) Mesokurtic - when kurtosis value = 0 . A normal distribution has a kurtosis value of  zero. It is in between the first two types.

Calculating the Kurtosis value

The formula for calculating kurtosis is shown below with an example. The sample size must be a least four. 

s = sample standard deviation

n = number of samples

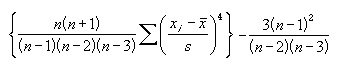
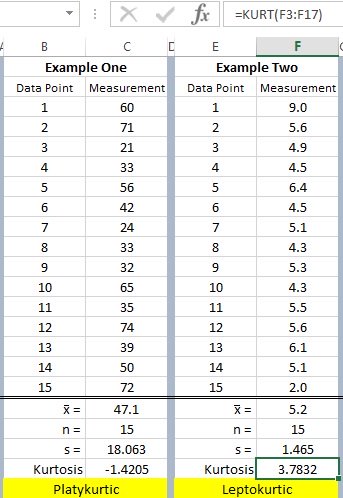
Examples

There are two sets of data shown with 15 samples each. The calculations are shown with the kurtosis value for each set. The formula in Excel is shown in the upper right.

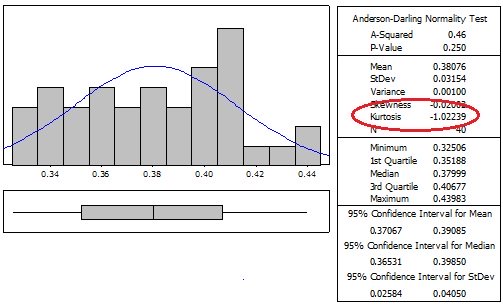
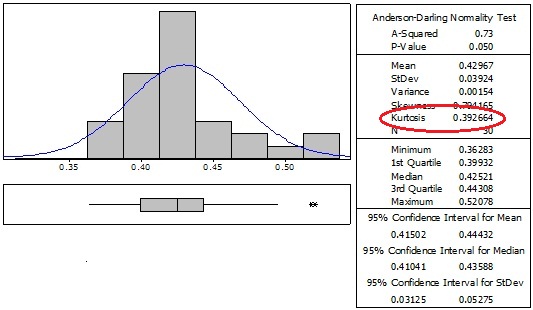
Other examples

Platykurtic 

Leptokurtic

Return to BASIC STATISTICS

Return to the ANALYZE phase

Templates and Calculators

Return to the Six-Sigma-Material Home page