Defects Per Million Opportunities (DPMO)

Defects per Million Opportunities factors in the total opportunities for defect occurrence existing in a process. DPMO is considered long-term measurement of a process and this can be directly converted into a long-term z-statistic (sigma value)

Given:

D: # of defects

O: # of opportunities for a defect

U: # of units

TOP: Total number of opportunities = U * O

Formula:

DPMO = DPO * 1,000,000

DPO = Defects per Opportunity

DPU = Defects per Unit

See the links or the example below to help understand the differences.

NOTE:

DPMO is NOT the same as PPM (parts per million) since it is possible that each unit (part) being appraised may be found to have multiple defects of the same type or may have multiple types of defects. A part is defective if it has one or more defects. The number of defectives can never exceed the number of defects.

If each part only has one characteristic that can be a defect, then DPMO and PPM will be the same.

You could have 1,000,000 defects on one part and the DPMO could be 1,000,000 and the PPM is 1.0 if that part is the only part out of the million that has any defects (in other words the other 999,999 parts have 0 defects). This is an exaggeration to try and illustrate the difference between DPMO and PPM.

Also keep in mind that it's possible that each widget being measured (or assessed) has a different amount of potential defects. So theoretically you could have just a few widgets (very complex widgets) that have thousands of opportunities for defects or a lot of simple widgets that only have a few total opportunities for defects.

PPM represents the number of defective parts (units) per 1 million units

DPMO is the number of defects per 1 million opportunities of defects

In summary, it is rare that a part can only have one defect type and therefore PPM and DPMO are often different measurements.

DPMO Example

Examine the table shown below:

Nail #1 has two types of defects. Therefore it is ONE defective nail that contains TWO defects.

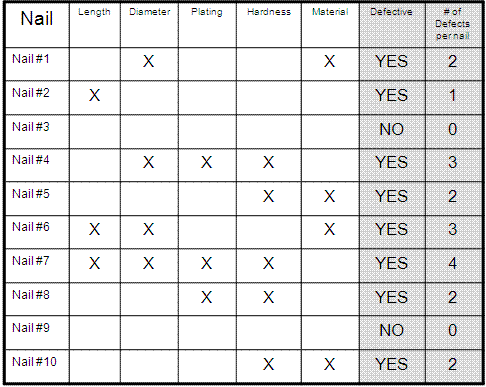
SUMMARY OF TABLE

D = 19 total defects

O = 5 opportunities (categories of defect types)

U = 10 nails

TOP = U * O = 50 total opportunities for defects

DPU = D / U = 19/10 = 1.9 defects per unit

DPO = D / TOP = 19/50 = 0.38

DPMO = 380,000

This result is saying that out of one million opportunities, the long-term performance of the process would create 380,000 defects.

Notice that only Nail #3 and Nail #9 had zero defects. Therefore 8 out of 10 nails had at least one defect. That represents a PPM of 800,000.

Want to convert a DPMO of 380,000 to a z-score? Read below or click here to learn more about z-scores (process sigma score).

ShareFacebook X WhatsApp Reddit

Using Excel to calculate Sigma and DPMO

There are a couple commonly used Microsoft Excel functions that converts Defects per Million Opportunities (DPMO) to a process sigma (z-score) and vice versa.

To convert from DPMO to process sigma:

Process Sigma (ZST) = -NORMSINV(DPMO/1,000,000)+1.5
Process Sigma (Z_LT) = -NORMSINV(DPMO/1,000,000)

To convert from process sigma to DPMO:

DPMO = 1000000*(1-(NORMSDIST*(process sigma-1.5))

To convert DPMO to % Defective

DPMO / 1000000*100 = % Defective

NOTE:

A Six Sigma quality process refers to the process short-term performance or how it is performing currently when there are 3.4 DPMO. Over the long term, this six sigma process is estimated to shift -1.5 sigma (lower) and will perform at a 4.5 sigma level, which produces 1,350 DPMO.

This +/- 1.5 sigma shift is an estimate. There is debate around this assumption since "short term" and "long term" are somewhat ambiguous terms. As the "short term" sample gets larger and larger and approaches a 'long-term" sample size, then the shift gets narrower too, this the 1.5 should be less than 1.5.

And vice versa, if the short term sample is very small then the shift may be -1.5, or even slightly more (such as -1.6), to get the assumed long terms process sigma.

See the screenshot below that summarizes how to write the formulas in Excel to go from DPMO, ZST, and ZLT.

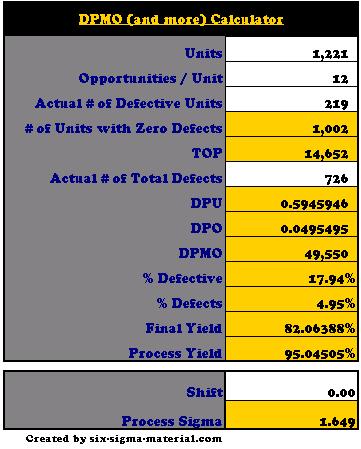
DPMO Calculator (Six Sigma Calculator)

Enter your values in the white cells and everything else is calculated. Notes are in the actual template that offer more guidance and information on each row.

This calculator can give you a Z_ST (if you input a shift of +1.5) or Z_LT score (if the shift is 0). This is shown at the bottom as the 'Process Sigma' value.