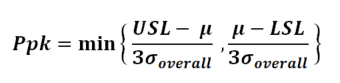Capability Index, Ppk

The capability indices of Ppk and Cpk use the mean and standard deviation to estimate probability. A target value from historical performance or the customer can be used to estimate the Cpm.

That spread being centered around the midpoint is part of the Cpk and Ppk calculations.

The midpoint = (USL- LSL) / 2

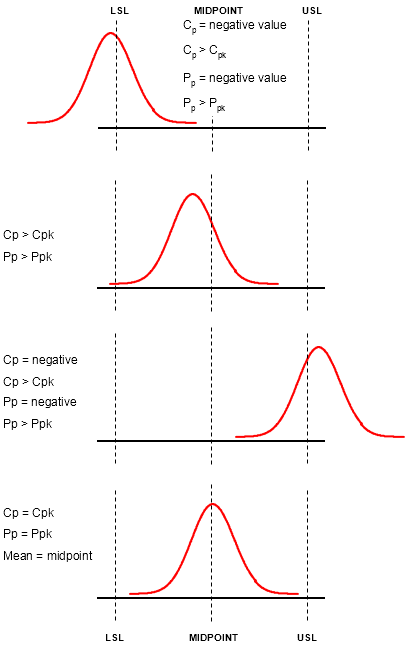
The addition of "k" quantifies the amount of which a distribution is centered. A perfectly centered process where the mean is the same as the midpoint will have a "k" value of 1.

Pp and Ppk use an estimate for sigma that takes into account all or total process variation including special causes (should they exist) and this estimate of sigma is the sample standard deviation, s, applies to most all situations. This estimation accounts for "within subgroup" and "between subgroup" variation.

Pp and Ppk calculation is the same as Cp and Cpk respectively. The difference is the method in which the standard deviation is calculated for Pp and Ppk.

The formula for the Ppk calculation and the standard deviation for use with Pp and Ppk is given below. Similar to Cpk, the minimum value of both calculations is used for Ppk.

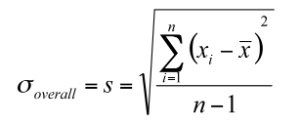
The Cpk and Ppk will require two calculations, selecting the minimum is the value use as baseline and to compare to customer acceptability level. These can be calculated using unilateral or bilateral tolerances.

The formula for Cpk and Ppk is for bilateral tolerances (where a LSL and USL are provided). If only one specification is provided (unilateral) then the value used for Cpk and Ppk is provided by the calculation that involves the specification limit provided.

Pp and Ppk are rarely used compared to Cp and Cpk. They should only be used as relative comparisons to their counterparts.

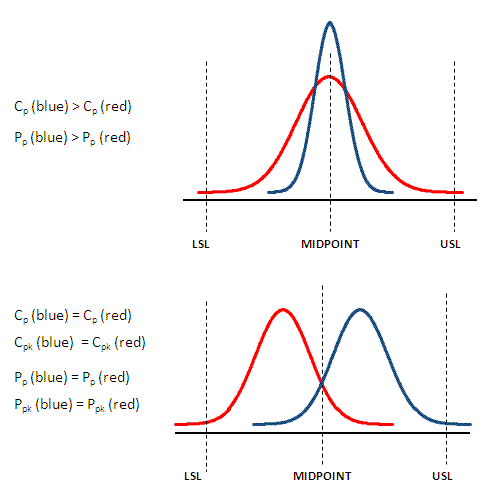
Capability indices, Cp and Cpk, should be compared to one another to assess the differences over a period of time. The goal is to have a high Cp, and get the process centered so the Cpk increases and approaches Cp. The same applies for Pp and Ppk.

Cpk indicates process capability on "short term" or "within subgroup" of data which is not inclusive of the effect of variation between the subgroups. Ppk takes into account both and is not limited to only the variation within each subgroups like Cpk.

The pitfall with Ppk is the variation within subgroups can not be separated so that is why it can help to use Cpk and Ppk to determine where the variation is coming from: within or between subgroups.

Cpk and Ppk account for centering of the process among the midpoint of the specifications.

However, this performance index may not be optimal if the customer wants another point as the target other than the midpoint. The calculation of Cpm accounts for the addition of a target value.

Takeaways for Cp, Cpk, Pp, and Ppk

Cp is a measurement of how tight the process variability is compared to the specifications. The higher the Cp, the tighter (or lower) the process variability.
Cpk is a measurement of how well the process is centered as well as the process variability (spread). The higher the Cpk, the better your process is and the less chance it has of creating defects.
A target value from historical performance or the customer can be used to estimate the Cpm.
Pp and Ppk are the same as Cp and Cpk respectively, except that Pp and Ppk are reflective of long term process performance.

Pp and Ppk are LONG TERM indices

Cp, Cpk, and Cpm are SHORT TERM Indices