Margin of Error
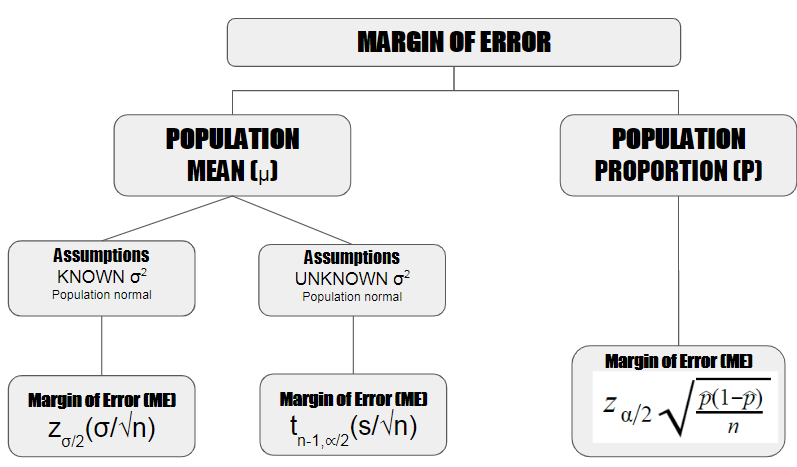
The Margin of Error (ME) is often expressed in the following formula as the Standard Error (SE) times an adjustment value which is a z-critical or t-critical value:
ME = critical value * Standard Error (SE)
Let's briefly discuss Standard Error.
SE of a statistic is the standard deviation of its sampling distribution or an estimate of that standard deviation. If the statistic is the sample mean, it is called the standard error of the mean. The standard error is an input for confidence intervals.
Standard error of the sample mean is an estimate of how far the sample mean is likely to be from the population mean, whereas the standard deviation of the sample is the degree to which individuals within the sample differ from the sample mean. Standard error of the mean is a statistical measure that estimates how likely the population mean is to differ from the sample mean.
Just like standard deviation, standard error is a measure of variability. However, the difference is that standard deviation describes variability within a single sample, while standard error describes variability across multiple samples of a population.
Standard Error Formulas
The population standard deviation is often not known and therefore a sample is drawn and the formula on the left is used and the SE is an estimate.
If the population is known, the exact value of SE can be calculated using the formula on the right.
Both formulas below assume an infinite population. There is a correction factor (not discussed here) if the population is known and finite. The larger the population the more meaningless the correction factor.
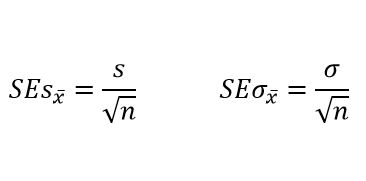
Standard Error Calculator
Standard Error vs. Standard Deviation
Experimental data are often summarized either using the mean and standard deviation of the sample data or the mean with the standard error.
- The mean and standard deviation are descriptive statistics,
- the standard error of the mean is descriptive of the random sampling process.
The standard error of the sample mean is an estimate of how far the sample mean is likely to be from the population mean, whereas the standard deviation of the sample is the degree to which individuals within the sample differ from the sample mean.
If the population standard deviation is finite, the standard error of the mean of the sample will tend to zero with increasing sample size, because the estimate of the population mean will improve, while the standard deviation of the sample will tend to approximate the population standard deviation as the sample size increases.
Getting back to Margin of Error
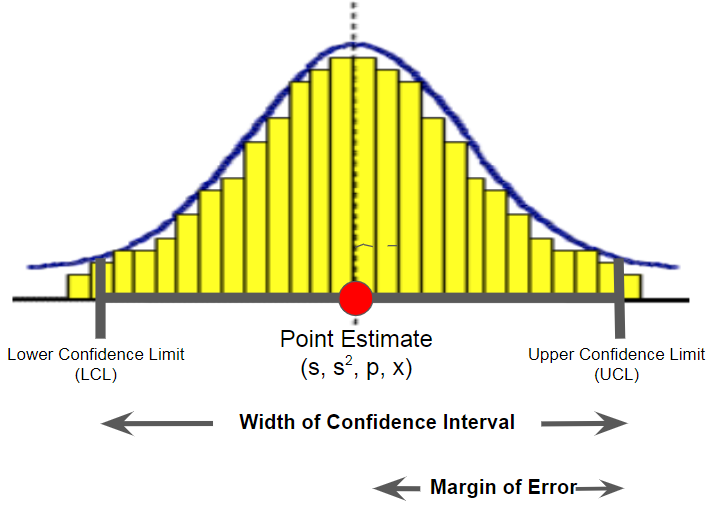
The ME is also sometimes called the maximum error of estimate or error tolerance. The ME is the "radius" or half the width of the confidence interval for a distribution. See below.
The ME is closely related to the calculation of a Confidence Interval (CI). The CI is:
- CI = point estimate (x-bar) +/- ME
- CI = point estimate +/- (critical value * Standard Error (SE))
- CI = x-bar +/- ME
Ways to REDUCE the Margin of Error:
- Increase the sample size, n
- Decrease the Confidence Level (same as saying increase the alpha-risk)
- Decrease the standard deviation
The larger the ME, the less confidence that the results represent those of the entire population. The larger the sample size, the smaller ME.
NOTE: When calculating the ME (and Confidence Intervals), the sample size should be <5% of the true population or a correction factor is needed which isn't discussed here (trying to keep it simple). These examples assume a large population that is not finite.
The most common calculations for the ME are shown below:
Margin of Error for a Mean and known σ
EXAMPLE:
if there were thousands of customers surveyed for a particular contractor and we sifted through a sampling of 125 of them and found the average rating was 4.26. Also, we know from the past that the population standard deviation is 0.21.
Calculate the Margin of Error for a desired 90% confidence level (or alpha risk of 10%)?
SOLVING:
In this case, we know the population standard deviation so we will use the z-critical value at risk of 0.10 or CL of 90% (same thing).
The z-critical value is 1.645 for 90% CL
The standard deviation of the sample = 0.21.
SE = the sample standard deviation / sqrt n = 0.21 / sqrt 125 = 0.21 / 11.18 = 0.01878 = SE
Therefore, the ME = 1.645 * 0.01878 = 0.0309 = ME
Margin of Error for a Mean and unknown σ
EXAMPLE:
if there were thousands of customers surveyed for a particular contractor and we sifted through a sampling of 125 of them an found the average rating was 4.26 with a sample standard deviation of 0.21.
Calculate ME for a 90% confidence level (or 0.10 alpha-risk = 10%)?
Now, we need to use the two-tailed t-table for 90% CL (or 0.10 risk) at a Degrees of Freedom of n-1 which = 124.
The t-critical value at 90% CL, dF = 124, is 1.657
(we used the calculator found here and a picture of it is below or you can use a table that shows the most commonly used values and interpolate from there)
The standard deviation of the sample = 0.21.
SE = the sample standard deviation / sqrt n = 0.21 / sqrt 125 = 0.21 / 11.18 = 0.01878 = SE
Therefore the ME = 1.657 * 0.01878 = 0.0311
Notice how close the answer is to the first example. The ME's are almost exactly the same. This is because the sample size is large and the t-critical approaches z-critical value as the sample size increases.
In this example, we will take it a step further and calculate the Confidence Interval (CI).
The center of the confidence interval, x-bar, is the point estimate. Take the point estimate and subtract the ME for the lower bound of the CI and add the ME to the point estimate to the upper bound of the CI.
It's that simple.
The x-bar value is 4.26, then the CI = {4.26 - 0.0311, 4.26 + 0.0311} = {4.2289, 4.2911}
In practical terms this means that you can be 90% certain that the population would choose a rating between 4.2289 to 4.2911 for that contractor.
If all things remain the same, the next result from the survey is 90% to have a result between 4.2289 and 4.2911. Obviously, most surveys don't ask for that level of resolution so there needs to be some reality check to the statistical answer....and this reality check applies to any statistical answer.
If you wanted a CL of 95% or 99%, the then margin for error increases since the critical value increase (in other words you want more confidence than 90% therefore you need to accept wider interval if you're going to keep the number of samples the same at 125).
Margin of Error for a population proportion
EXAMPLE:
If there were a sampling of 100 people and 20 of them voted yes on a new regulation, calculate the Margin of Error for a 95% confidence level (or 0.10 alpha-risk = 10%)?
The following formula assumes that nP(1-P) > 5 (which essentially says that the sample size is <5% of the total true population).
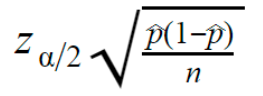
The z-critical value is 1.645 for 95% CL
p-hat = 0.20 = the sample proportion
n = 100
SE = sqrt ((0.20(1-0.20)) / 100) =sqrt ((0.20*0.80)/100) = sqrt (0.16/100) = sqrt 0.0016 = 0.04 = SE
Therefore, the ME = 1.645 * 0.04 = 0.0658
NOTE: In this case the ME is a percentage but not in the previous two examples. Be careful when expressing ME as a percentage.
Therefore, the Margin of Error = 6.58%
The Confidence Interval (CI) is calculated as follows:

p-hat = 20/100 = 0.20
CI = 0.20 +/- 0.0658 = {0.1342 , 0.2658}
CI = 20% +/- 6.58% = {13.42% , 26.58%)
You can be 95% confident that the true percentage of people that will vote yes is between 13.42% and 26.58%.
Although there is chance the the interval of 13.42% to 26.58% may not contain the true proportion, 95% of confidence intervals created will contain the true proportion.
ME for Means of TWO RELATED Populations
To test the MEANS of two related populations these are considered dependent samples. This takes away the variation among the subjects. This section assumes:
- Sample measurements are Before/After, Repeated, Paired, or Matched
- Both populations are normally distributed (or meet normality assumption)
The following formulas apply:
the ith paired difference is: di = xi - yi
d-bar is the point estimate used to calculate the confidence interval.
n = number of matched pairs in the sample.
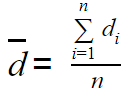
The sample standard deviation in this case is:
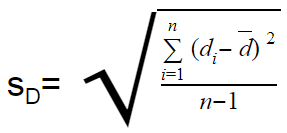
The formula is the same as the Means for a sample except the standard deviation is considerate of both samples instead of one sample and denoted sD

For the Confidence Interval, the point estimate is d-bar +/- ME.

Margin of Error Calculator
|
Download a Margin of Error calculator, along with several others, with examples. Click here to see all the Templates and Calculators that can help further understand these topics and accelerate the execution of a Six Sigma Project. |
Margin of Error & Sample Size
You can see how many common terms are related now. Once you have the ME, the Confidence Interval calculation is easy. The hardest part is calculating the ME.
Sometimes you may have a desired ME or may be given a directive not to exceed a certain ME. In that case you can adjust scenarios to find out what Sample Size is necessary at various Confidence Levels.
Rearrange the formula and solve for n. Then plug in the desired ME and Confidence Level and you'll get the minimum sample size required....and round up the answer to the nearest whole number.
Return to Confidence Intervals
Search active job openings in Six Sigma
Return to the Six-Sigma-Material.com home page
Recent Articles
-
Process Capability Indices
Oct 18, 21 09:32 AM
Determing the process capability indices, Pp, Ppk, Cp, Cpk, Cpm -
Six Sigma Calculator, Statistics Tables, and Six Sigma Templates
Sep 14, 21 09:19 AM
Six Sigma Calculators, Statistics Tables, and Six Sigma Templates to make your job easier as a Six Sigma Project Manager -
Six Sigma Templates, Statistics Tables, and Six Sigma Calculators
Aug 16, 21 01:25 PM
Six Sigma Templates, Tables, and Calculators. MTBF, MTTR, A3, EOQ, 5S, 5 WHY, DPMO, FMEA, SIPOC, RTY, DMAIC Contract, OEE, Value Stream Map, Pugh Matrix

Site Membership
LEARN MORE
Six Sigma
Templates, Tables & Calculators
Six Sigma Slides
Green Belt Program (1,000+ Slides)
Basic Statistics
Cost of Quality
SPC
Control Charts
Process Mapping
Capability Studies
MSA
SIPOC
Cause & Effect Matrix
FMEA
Multivariate Analysis
Central Limit Theorem
Confidence Intervals
Hypothesis Testing
Normality
T Tests
1-Way ANOVA
Chi-Square
Correlation
Regression
Control Plan
Kaizen
MTBF and MTTR
Project Pitfalls
Error Proofing
Z Scores
OEE
Takt Time
Line Balancing
Yield Metrics
Sampling Methods
Data Classification
Practice Exam
... and more