Poisson Distribution

The Poisson Distribution is a discrete distribution named after French mathematician Simeon-Denis Poisson.

Unlike the Binomial Distribution that has only two possible outcomes as a success or fail, this distribution focuses on the number of discrete occurrences over a defined interval. It is used to estimate the probabilities of events that occur randomly per some unit of measure.

This formula describes rare events and is referred to as the law of improbable events. The formula shown below calculates the probability of occurrences over an interval.

It can provide an approximation to the Binomial Distribution if the number of samples (n) is large and probability of a success (p) is small.

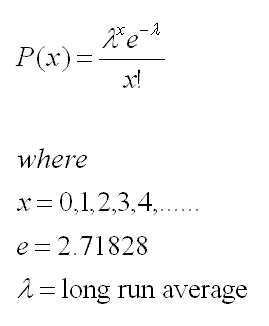
The Poisson distribution exhibits the following:

discrete distribution (such as 0,1,2,3,4...)

occurrences are independent of each other

occurrences range from 0 to infinity in an interval

describes rare events

describes discrete occurrences of defined interval

expected number of occurrences must be constant in a Poisson experiment, this is the value of lambda (λ) which must be a positive real number.

Lambda (λ) = n*p (sample size * probability) = population mean 

λ is the only parameter that Poisson distribution depends on. 

The smaller the value of λ, the more biased the data distribution.

The data distribution tends to be symmetric as Lambda gets larger and a Lambda of 20 tends to result in a normal distribution.

The Poisson Distribution may apply when studying the:

number of customers per minute in a bookstore

number of transactions per hour at a bank

number of long distance telephone calls per day

number of cracks per windshield

number of cars passing through an intersection per day

number of late shipments per 1,000 shipments

number of bugs per byte of code

number of pieces scrapped per 1,000,000 pieces produced

number of planes arriving per hour at airport

number of sick days per month (or vacation days per...,  tardy days per...)

number of vacant houses per county in a state

number of defects found per form

number of insurance claims per year

number of airplane accidents at an airport over time

defects per unit (DPU)

Notice the word "per" in each of the above statements. 

---

Relationship to Exponential Distribution

A random variable that has a Poisson distribution must have a probability, p, of occurrence that is proportional to the interval length. The number of occurrences in an interval must also be independent events.

Both the Poisson distribution and Exponential distribution are used to to model rates but the latter is used when the data type is continuous.

The Exponential distribution has a Poisson distribution when the:

1. event can occur more than 1 time
2. time between two successive occurrences is exponentially distributed
3. events are independent of previous occurrences

If the random variable, x, has an Exponential distribution then the reciprocal (1/x) has a Poisson distribution.

The Poisson Distribution is applied to model the number of events (counts) or occurrence per interval or given period (could be arrivals, defects, failures, eruptions, calls, etc.). This models discrete random variables.

The Exponential distribution is applied to model the mean time (such as waiting times) between occurrences, time is a continuous variable.

---

Example using Poisson Distribution

A new website has an average random hit rate of 2.9 unique visitors every 4 minutes. What is the probability of getting exactly 50 unique visitors every hour?

Given information:

---

Recommended video on the Poisson Distribution

---

Return to BASIC STATISTICS

Templates, Statistics Tables, and Calculators

Subscribe to access all pages

Return to the Six-Sigma-Material Home Page