Measures of Central Tendency

Mean, Median, Mode

In a normally distributed set of data, all three measures of central tendency are approximately the same. Using the data sample below, calculate the measures of central tendency.

{1, 3, 8, 3, 7, 11, 8, 3, 9, 10}

Mean (arithmetic)

Since most populations exhibit normality (bell-shaped curve) or can be assumed to be normal, the mean is the most common measure for central tendency. It is used to describe normal data.

The formula is the summation of all the values divided by the sample size:

Sum of all values: 63

n: 10 samples

Mean = 6.3

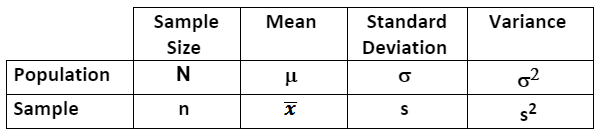
In this example, the mean is of a sample which is represented by x-bar. Sometimes M is also used to represent the sample mean. For a population mean, the Greek letter μ is used. See the table below for common notation.

Median

The median is the midpoint, the middle value or observation of the data set. If the set of data has an even count, the median is the average of the middle two values. This is measure for skewed or non-normal data.

Arrange the numbers in ascending or descending order:

{1, 3, 3, 3, 7, 8, 8, 9, 10, 11}

Since the sample is an even set of data (10 samples) and the middle two values are 7 and 8, then the average of the two middle values is 7.5.

Median = 7.5

Mode

The mode is the most commonly occurring value in the data set. Not commonly used as a measure of central location but can be found in the tallest bar of a vertical histogram chart.

Mode = 3, since it occurs more than any other value.

The table below summarizes notation for describing samples and populations.

Samples are properly described as statistics.
Populations are properly described as parameters.

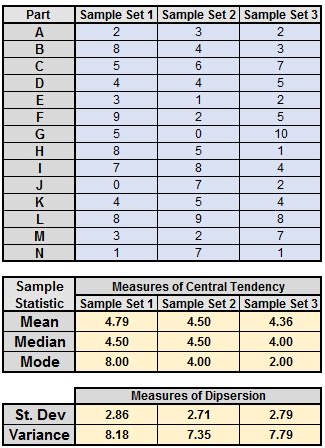
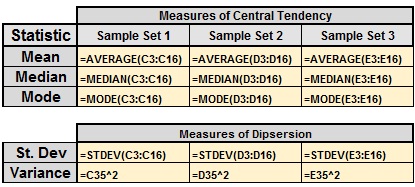
Another example using Excel

Showing the formulas

For the Standard Deviation, Excel uses "n-1" in the denominator to calculate the sample statistics (the rows in Excel for the data were in rows 3-16).

Trimmed Mean

The trimmed mean is another measure of central tendency less frequently used but you may see it as an output on most statistical software programs.

This is a mean calculated by excluding a percentage of data points from the top and bottom tails of a data set. Usually 5% is trimmed off of each tail. But sometimes you can specify the percentage to trim.

The % value can not be <0 or >1.

In Excel, you can select the array of data and choose a % to trim off each tail using the TRIMEAN function.

TRIMMEAN(array, percent)

Array - the array or range of values to trim and average.

Percent - The fractional number of data points to exclude from the calculation. For example, if percent = 0.2, 4 points are trimmed from a data set of 20 points (20 x 0.2): 2 from the top and 2 from the bottom of the set.

NOTE:

This function rounds the number of excluded data points down to the nearest multiple of 2. If percent = 0.1, 10 percent of 30 data points equals 3 points. For symmetry, TRIMMEAN excludes a single value from the top and bottom of the data set.

Measures of dispersion are numerical statistics which describe the spread of data or the width of the distribution.

NOTE:

A normal distribution exhibits a mean, median, and mode that are approximately the same value.