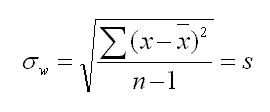Degrees of Freedom (dF)

Objective:

The term Degrees of Freedom (dF) is used in statistics to calculate the number of measurements that are needed to make an unbiased estimate of a statistic. It is the number of independent pieces of information available to estimate a statistic.  Also defined as the number of values that may vary in the final calculation of a statistic. 

An "unbiased estimate" is when the mean of the sampling distribution of a statistic can be shown to equal the (population) parameter being estimated.

The more degrees of freedom, the lower the uncertainty in your results....which is similar to the sample size (the more samples, the more representative of the population, thus less uncertainty in your results). Therefore, dF and 'sample size' are not equal but they are related. 

The dF characterize the uncertainty in the estimated sigma which determines the amount of uncertainty in calculated control limits. 

The dF is represented by the lowercase Greek letter nu (v).

dF  = n - x

where n is the sample size or observations and x is number of parameters to be estimated.

An example of a "parameter to be estimated" is the sample mean when calculating the sample standard deviation as shown below.

A simple way to generalize it is as the number of samples minus the number of calculated (estimated) parameters.

The dF in this case is equal to n-1 since only the sample mean is being estimated. In other words, the sample variance contains n-1 degrees of freedom. There a "n" random values minus the sample mean which is estimated. 

dF formulas:

dF = n-1 when using the Paired t-test and 1-Sample t test.

dF = n1 + n2 - 2 when using the 2-Sample t test with assumed equal variances

dF = (# of Rows - 1) * (# of Columns - 1) when using chi-square tests

Notation:

There are a few variations used to denote degrees of freedom:

v = lower case Greek letter nu which is most commonly found in equations

n = however this is more often applied to represent sample size

d.f. or dF

Practice Problem

The chi-square test is being used to analyze the results of an experiment which had 6 treatments and each treatment was categorized as one of two options, PASS or FAIL.

How many degrees of freedom are used to compare calculated chi-square and tabulated chi-square values?

Answer:

dF = (# of Rows - 1) * (# of Columns - 1)

dF = (2-1) * (6-1) = 1 * 5 = 5

ShareFacebookXWhatsApp

Return to Basic Statistics

Proceed to the IMPROVE phase

Templates, Tables, and Calculators

Return to the Six-Sigma-Material Home Page