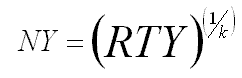Normalized Yield (NY)

Normalized Yield (NY) is the average yield per process step. It's the probability of a unit passing through one process step or opportunity without rework. It's the minimum Throughput Yield (TPY) for each step of the process to achieve a given Rolled Throughput Yield (RTY).

NY is used when the TPY is not known for each step of a process but the RTY for the entire process is known. Recall, if the TDU is known, the RTY can be found and then the NY can be determined, click here to review.

Then the NY is used to assume each step of the process has the same average yield.

CAUTION: Applying that logic can be misleading since true yields at each step can be significantly different. This is sometimes referred to as the "typical" yield. These yield metrics can be inaccurate with skewed distributions or heavy tailed distributions...in other words distributions that are not normal.

Formula:

where k equals the number of processes.

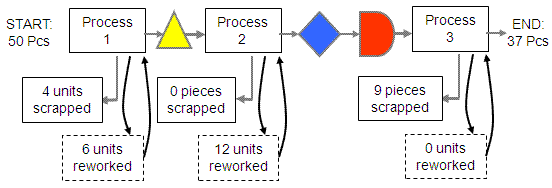
A calculation using example from above:

Calculation:

Using k = 3

NY = 0.476^(1/3)

NY = 0.781 = 78.1%

There is a 78% chance of a unit passing through one process step without rework.

Another relationship is shown below to obtain the normalized defects per unit.

The normalized defects per unit equals -ln(0.781) = 0.24718.

Normalized Yield and other yield metrics can serve as baseline scores (Measure Phase) and final scores for Six Sigma projects (Control Phase).

The baseline score does not have to be a z-score and often these yield metrics are easier for team and other company employees to relate with and understand.

Converting to Z-benchmark score

Z_benchmark = Z_NY + 1.5 (assumed shift to short-term or "best-case" performance)

The z-value of 0.24718 using an approximation from a standard normal curve z table = 0.686.

Therefore,

Z_benchmark = 0.686 + 1.5 = 2.186