Binomial Distribution

The binomial distribution is a discrete distribution displaying data that has only TWO OUTCOMES and each trial includes replacement. The binomial distribution approaches a normal distribution as the sample size increases; therefore, this approximation is better for larger sample sizes.

Example are options such as:

PASS / FAIL
GO / NO-GO
SUCCESS / FAILURE
IN / OUT
YES / NO
HOT / COLD
MALE / FEMALE
WORKS / DOESN'T WORK
DEFECTIVE / NOT DEFECTIVE
RIGHT-HANDED / LEFT-HANDED
HIGH / LOW
CORRECT / INCORRECT
HEADS / TAILS

Assumptions

Each trial has only two outcomes
The experiment has n identical trials
Each trial is independent of the other trials
The probability of getting one outcome (success) p is held constant and the probability of getting the other outcome (failure) is also held constant, represented by (1 - p) also referred to as q.
Includes replacement for each trial. It can be used to approximate without replacement trials but it is suggested to use hypergeometric distribution formulas.

Let's evaluate the assumptions:

A coin flip is an example of two outcomes and each flip has the same chance for both outcomes (meaning independent). Flipping the coin n amount of times means there are n identical and independent trials. Nothing changes from one flip to another and the odds are the same for each flip.

Binomial Distribution Central Tendencies

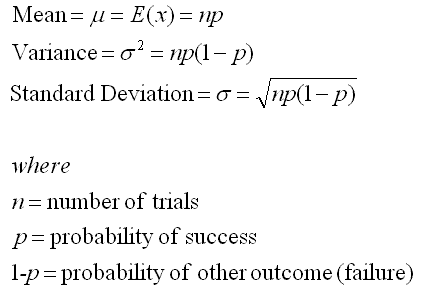
The following formula is used to compute the number of experimental outcomes resulting from x successes in n trials.

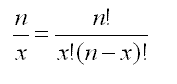
For example: 4! (4 factorial) = 4*3*2*1 = 24

The Binomial Distribution Probability Function is shown below:

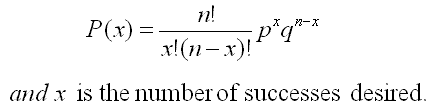
Binomial Distribution Example

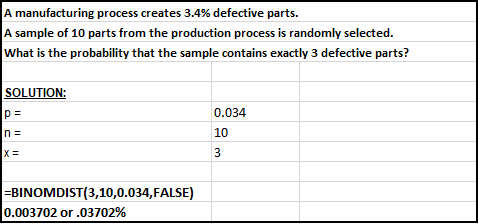
A manufacturing process creates 3.4% defective parts. A sample of 10 parts from the production process is randomly selected. What is the probability that the sample contains exactly 3 defective parts?

SOLUTION:
There are two outcomes: Defective / Not-Defective, therefore the Binomial Distribution equation is applied.

p = 0.034 (which is 3.4%)
n = 10 samples
then q = 1-p = 1 - 0.034 = 0.966 (which is 96.6%)
Need the probability that x = 3.

Substitute the values into the Binomial Probability Function and solve:

Example One of applying the Binomial Distribution

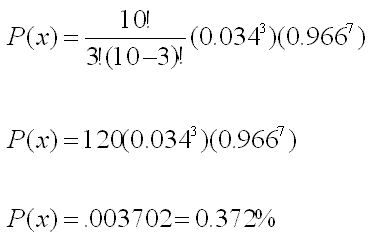
The picture below shows how to solve the problem using Excel

Example Two

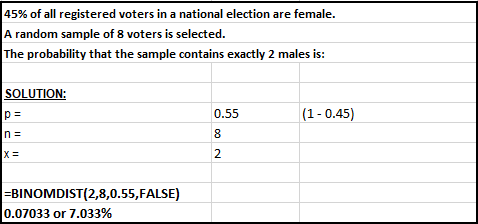
45% of all registered voters in a national election are female. A random sample of 8 voters is selected. The probability that the sample contains exactly 2 males is:

SOLUTION:
55% are male and there are two outcomes: MALE / FEMALE
n = 8
p = 0.55 (55%)
q = 1-p = 0.45 (45%)
Need the probability that x = 2

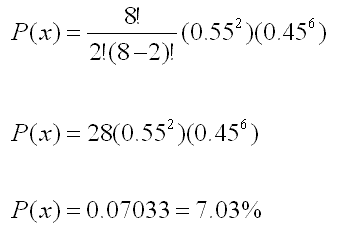
The picture below shows how to solve the problem using Excel

Example Three

79% percent of the students of a large class passed the final exam. A random sample of 4 students are selected to be analyzed by the school. What is the probability that the sample contains fewer than 2 students that passed the exam?

There are two outcomes: PASS / FAIL

p = 0.79
n = 4

Solving for the probability that x < 2.

Note that we need to compute p(x<2). So, it is necessary to add the P(x=0) to the P(x=1).

Each P(x=0) and P(x=1) must be calculated separately and added.

p(x<2) = p(x=0) + p(x=1)

Substitute the following values into the binomial equation to find p(x=0):

n = 4
p = 0.79
q = 1 - p = 1 - 0.79 = 0.21
x = 0

PLUS

n = 4
p = 0.79
q = 1 - p = 1 - 0.79 = 0.21
x = 1

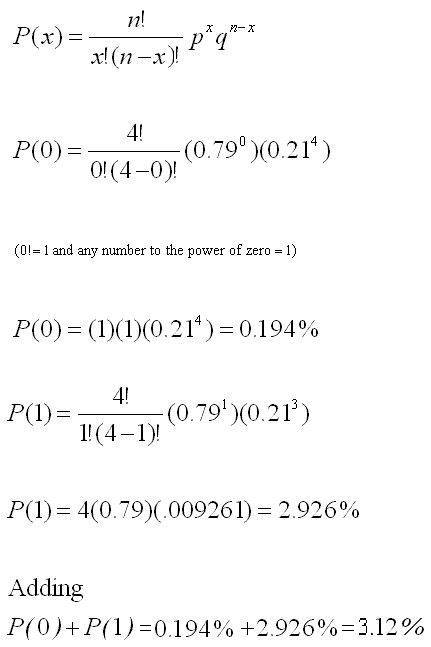
The picture below shows how to solve the problem using Excel

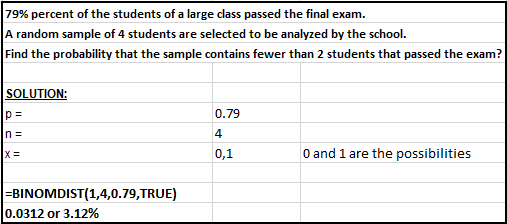
There is 3.12% chance of selecting fewer than 2 (in other words, 0 or 1 student) students that passed the exam when randomly selecting 4 students when 79% of them passed.

There are also Binomial tables that can be used when the input variables are known (and found within the table).