Yield to Sigma Relationship

The probability of having a defect in Process 1:

P(1) = 1 – TPY

Simply says that 100% minus the % of not having a defect from either scrap or rework in ONLY Process 1 is the probably of having a defect.

P(1) = 1 – 0.80 = .20 = 20%

Z-table for 0.20 is approximately 0.84 sigma. This is considered a long term sigma value.

For an entire series of processes use the RTY in place of TPY above. The probability of having a defect in the entire series is:

P(All) = 1 – RTY = 1 – 0.475 = 0.525 = 52.5%

z-table for 0.525 is less than 0 sigma, long term which indicates over half will be defective.

A negative sigma value means that most of the process is performing outside your customer's specification range (LSL and USL).

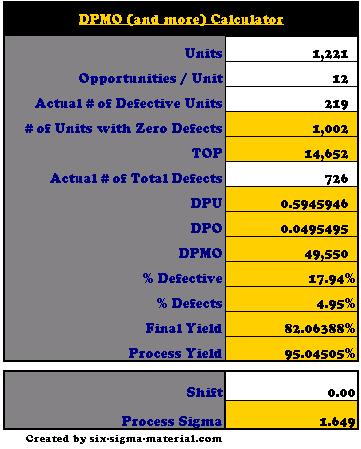
Using Excel to calculate DPMO and Sigma

There are a couple commonly used Microsoft Excel functions that convert Defects per Million Opportunities (DPMO) to a process sigma (z-score) and vice versa.

To convert from DPMO to process sigma:

Process Sigma = NORMSINV * ( 1 - ( DPMO / 1,000,000)) + 1.5

To convert from process sigma to DPMO:

DPMO = 1,000,000 * ( 1 - ( NORMSDIST * (process sigma - 1.5 ))

CAUTION:

The 1.5 shift is subjective, but some experts use this as conversion from long to short term performance estimates (and vice versa).

NOTE:

A Six Sigma process refers to the process short-term performance or how it is performing currently. When referring to DPMO of the process, we are referring to long-term or projected performance behavior.

A six sigma level of performance has 3.4 defects per million opportunities (3.4 DPMO). A current six sigma process now will have a estimated shift of 1.5 sigma (lower) in the future and will perform at a 4.5 sigma level, which produces 3.4 DPMO.