Future Value of Money (FV)

Calculating Future Value of Money is a very important concept in one's investment lifetime and also relevant to many Six Sigma projects...and may show up on a Six Sigma certification exam. 

Calculating FV is an important concept to project a future amount based on inputs of expected interest rate, number of time periods, beginning amount, and payments for the period. (assumed constant over each period).

FV is the value of a current asset (or amount of money) at some point in the future based on an assumed growth rate. There are two commonly used formulas:

1) The basic formula for simple interest (not compounding) is 

FV = I * (1 + (R * T))

where

• I = initial investment amount (or current asset value) or present value
• R = annual interest rate
• T = number of years 

The time interval could be 'months' or any time interval as long as they are the same units  for R and T.

Example One:

What is the FV of a $10,000 investment after 8 years that earns 5% simple interest annually? 

FV = 10,000 * (1 + (0.05 * 8))

FV = 10,000 * (1 + 0.4) 

FV = 10,000 * 1.4 = $14,000

2) The basic formula for compounding interest is shown below:

FV = I * (1 + R)^T

where

• I = initial investment amount (or current asset value) or present value
• r = annual interest rate
• n = number of periods interest is held

Example Two:

Using the same example for 1) but using compounding interest. What is the FV of a $10,000 investment after 8 years that earns 5% compounding interest annually? 

FV = 10,000 * (1 + 0.05)⁸

FV = 10,000 * (1.05)⁸ 

FV = 10,000 * 1.477 = $14,770

The final result between 1) and 2) is an increase of $770 over eight years as a result of compounding interest (i.e., earning interest on the interest earned from the previous time period) each year instead of solely simple interest. 

More advance compounding interest example

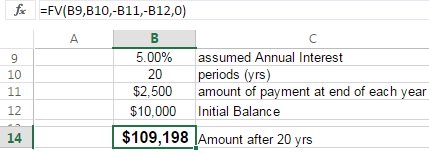
The following is more complex example done in Excel with the following assumptions:

• 5% annual interest rate
• Plan to make 20 payments at end of each year for 20 years.
• Using Excel means that a '0' is used for this input.
• The amount of the payment added at the end of each year is $2,500
• The amount at the beginning is $10,000 (present value)
  

The answer is $109,198. The ability to run scenarios with money that is freed up from a project is useful to help make investment decisions.

This obviously has a very practical use in personal lives as well. The above example is similar to a savings plan for a child's college tuition.

The picture below shows the FV formula and how to enter into Excel.

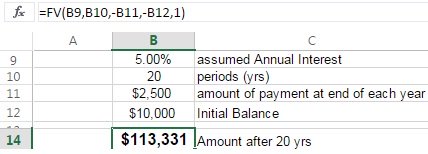
If you made the $2,500 at the beginning of each year, then you would enter a '1" into the formula as shown below instead of the '0' at the end. 

Notice the value has grown from $109,198 to $113,331 which seems logical since more time is allowed for the additional money to grow and thus also compound. 

Get this .pdf module that also covers ROI, ROA, Payback period, IRR, and NPV. All in all, the Training Slides include 1000+ Six Sigma training slides to allow you to prepare yourself about the DMAIC methodology and ultimately help you pass the certification exam.  Click here to review all the materials included.

Learn more about the Financial Savings types

Strategies to close out your project quickly

Start at DMAIC

Six Sigma Practice Questions