ShareFacebookTwitterWhatsApp

The following assumptions and rules apply to use the Hypergeometric Distribution:

• Discrete distribution.
• Population, N, is finite and a known value.
• Two outcomes - call them SUCCESS (S) and FAILURE (F).
• Number of successes in the population is known, S.
• Used when sample size, n, is greater than or equal to 5% of N.
• Trials are done without replacement, dependent.

A random variable (x) follows this distribution if its probability mass function is given by the formula shown below:

Hypergeometric Distribution at Six-Sigma-Material.com

Example

A sample of 5 parts are drawn without replacement from a total population of 30 parts. Determine the probability of getting exactly 2 defective parts. The population is known to have 14 defective parts.

Solving:

There are two outcomes and n/N = 5/30 = 16.6% which satisfies assumptions.

• n = sample size = 5
• N = population = 30
• s = "successes from sample" = 2
• S = "successes from population = 14

Substitute the values above into the probability formula above:

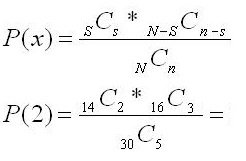
The probability of getting exactly 2 defective parts is 0.3576 or 35.76%

The denominator represents the total amount of combinations of selecting 5 parts from 30 parts, which is 142,506 for this example.

Keep in mind, this says "defective" parts. Each part may have one or more "defects" that cause the part to be appraised as a "defective" part. There is a difference between and defective part and a defect on a part. 

Using Excel

Most statistical software programs can solve for probabilities when given the correct inputs. Entering the data correctly can be tricky so be sure to review the examples or 'help' sections within the software. 

Return to BASIC STATISTICS

Return to other Discrete Distributions

Templates, Table, and Calculators

Subscribe to access all pages within this site

Return to Six-Sigma-Material Home Page